How Can You Tell if a Graph Is a Function
Learning Outcomes
- Verify a function using the vertical line examination
- Verify a one-to-1 function with the horizontal line test
- Identify the graphs of the toolkit functions
As we take seen in examples higher up, we can represent a function using a graph. Graphs display many input-output pairs in a pocket-size space. The visual information they provide often makes relationships easier to understand. Nosotros typically construct graphs with the input values forth the horizontal axis and the output values along the vertical axis.
The virtually common graphs proper name the input value [latex]x[/latex] and the output value [latex]y[/latex], and we say [latex]y[/latex] is a function of [latex]x[/latex], or [latex]y=f\left(x\correct)[/latex] when the function is named [latex]f[/latex]. The graph of the function is the fix of all points [latex]\left(10,y\correct)[/latex] in the plane that satisfies the equation [latex]y=f\left(x\right)[/latex]. If the function is defined for only a few input values, so the graph of the role is only a few points, where the x-coordinate of each point is an input value and the y-coordinate of each betoken is the corresponding output value. For example, the blackness dots on the graph in the graph below tell us that [latex]f\left(0\correct)=two[/latex] and [latex]f\left(6\correct)=1[/latex]. However, the set of all points [latex]\left(x,y\right)[/latex] satisfying [latex]y=f\left(x\correct)[/latex] is a curve. The curve shown includes [latex]\left(0,2\right)[/latex] and [latex]\left(6,1\right)[/latex] because the curve passes through those points.
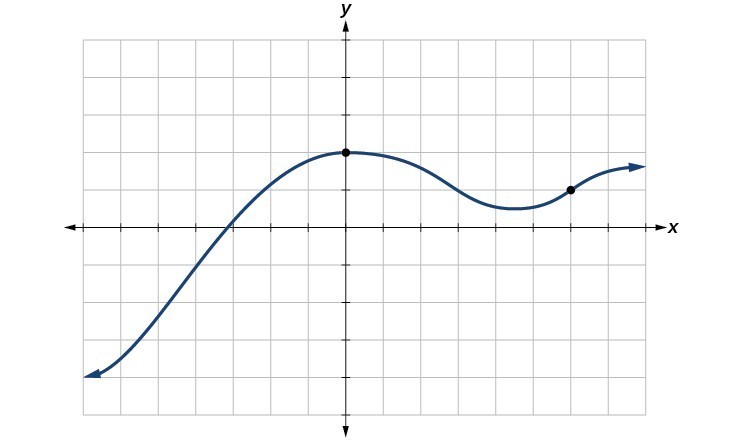
The vertical line exam tin can be used to decide whether a graph represents a part. A vertical line includes all points with a particular [latex]x[/latex] value. The [latex]y[/latex] value of a indicate where a vertical line intersects a graph represents an output for that input [latex]x[/latex] value. If we can draw any vertical line that intersects a graph more than than once, and so the graph does non define a function because that [latex]x[/latex] value has more than than 1 output. A function has just one output value for each input value.
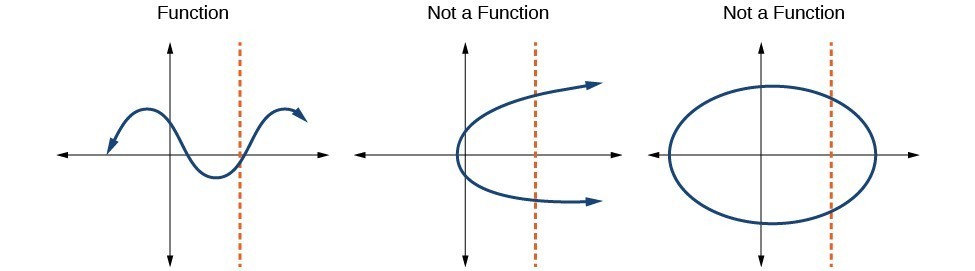
How To: Given a graph, employ the vertical line test to determine if the graph represents a function.
- Audit the graph to see if any vertical line drawn would intersect the curve more once.
- If in that location is any such line, the graph does not correspond a function.
- If no vertical line can intersect the bend more than once, the graph does represent a function.
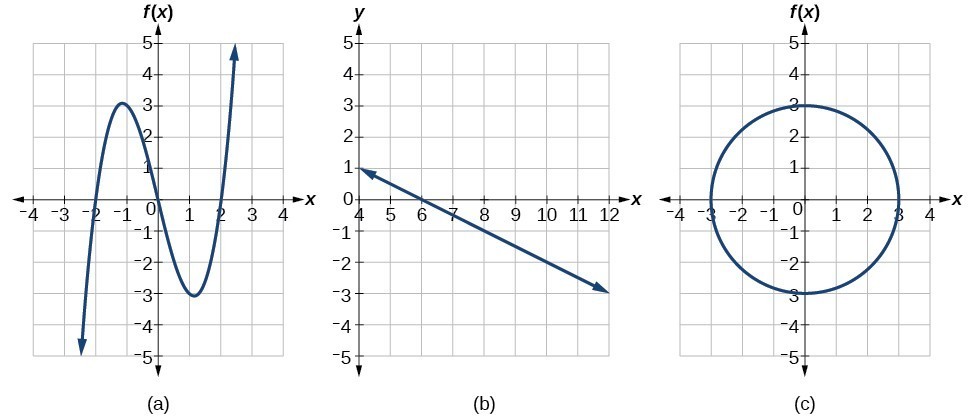
Example: Applying the Vertical Line Test
Which of the graphs represent(s) a function [latex]y=f\left(x\right)?[/latex]
Effort It
Does the graph below correspond a office?
The Horizontal Line Test
In one case nosotros take adamant that a graph defines a function, an easy fashion to determine if information technology is a one-to-ane function is to use the horizontal line test. Draw horizontal lines through the graph. A horizontal line includes all points with a detail [latex]y[/latex] value. The [latex]ten[/latex] value of a signal where a vertical line intersects a function represents the input for that output [latex]y[/latex] value. If we tin draw whatever horizontal line that intersects a graph more than than one time, and then the graph does not represent a function because that [latex]y[/latex] value has more than one input.
How To: Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one role.
- Inspect the graph to see if any horizontal line drawn would intersect the bend more in one case.
- If there is any such line, the function is not one-to-one.
- If no horizontal line tin can intersect the bend more than once, the function is one-to-one.
Instance: Applying the Horizontal Line Test
Consider the functions (a), and (b)shown in the graphs below.

Are either of the functions one-to-one?
Identifying Basic Toolkit Functions
In this text we explore functions—the shapes of their graphs, their unique characteristics, their algebraic formulas, and how to solve problems with them. When learning to read, we start with the alphabet. When learning to practice arithmetic, nosotros first with numbers. When working with functions, information technology is similarly helpful to have a base of operations set of building-block elements. We call these our "toolkit functions," which class a set of basic named functions for which we know the graph, formula, and special backdrop. Some of these functions are programmed to individual buttons on many calculators. For these definitions nosotros volition utilise [latex]x[/latex] as the input variable and [latex]y=f\left(10\correct)[/latex] every bit the output variable.
We volition run across these toolkit functions, combinations of toolkit functions, their graphs, and their transformations frequently throughout this book. It will be very helpful if we tin can recognize these toolkit functions and their features speedily by name, formula, graph, and basic table properties. The graphs and sample table values are included with each function shown beneath.
| Toolkit Functions | ||
|---|---|---|
| Proper name | Office | Graph |
| Constant | [latex]f\left(x\right)=c[/latex], where [latex]c[/latex] is a abiding | 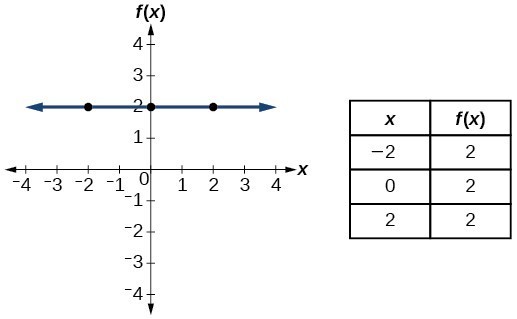 |
| Identity | [latex]f\left(10\right)=10[/latex] |  |
| Accented value | [latex]f\left(x\right)=|10|[/latex] | 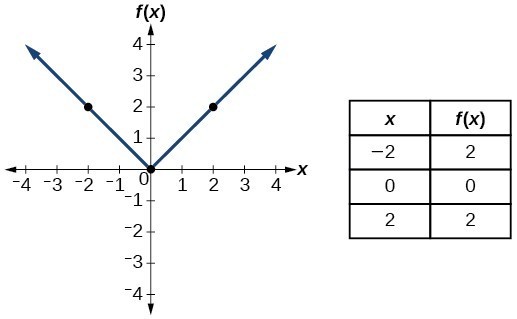 |
| Quadratic | [latex]f\left(10\right)={ten}^{two}[/latex] |  |
| Cubic | [latex]f\left(x\right)={10}^{three}[/latex] | 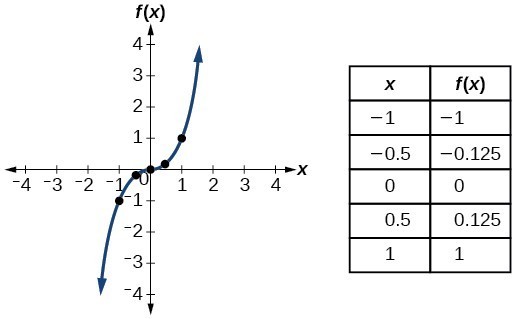 |
| Reciprocal/ Rational | [latex]f\left(ten\correct)=\frac{1}{10}[/latex] | 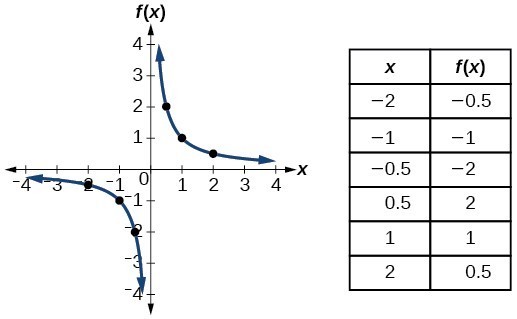 |
| Reciprocal / Rational squared | [latex]f\left(x\correct)=\frac{i}{{x}^{2}}[/latex] | 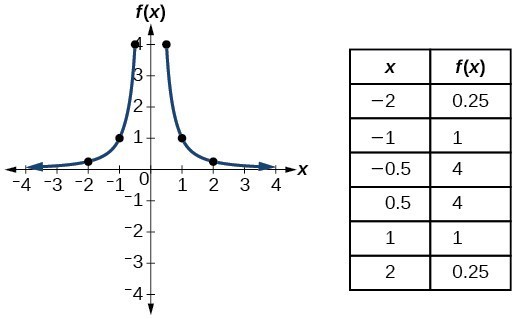 |
| Square root | [latex]f\left(10\right)=\sqrt{x}[/latex] | 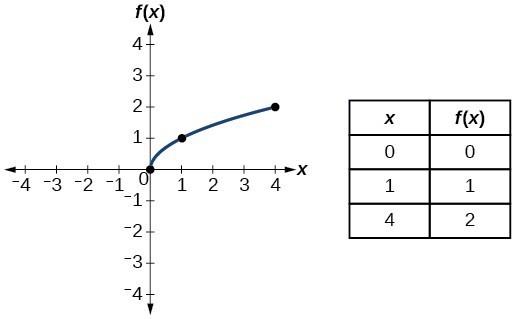 |
| Cube root | [latex]f\left(x\right)=\sqrt[3]{10}[/latex] | 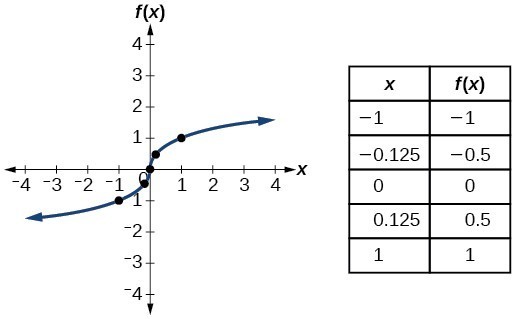 |
Endeavour It
Try Information technology
In this exercise, you will graph the toolkit functions using an online graphing tool.
- Graph each toolkit part using role notation.
- Brand a table of values that references the role and includes at least the interval [-5,5].
Contribute!
Did you have an idea for improving this content? We'd beloved your input.
Ameliorate this pageLearn More
Source: https://courses.lumenlearning.com/waymakercollegealgebra/chapter/identify-functions-using-graphs/#:~:text=Inspect%20the%20graph%20to%20see,graph%20does%20represent%20a%20function.
0 Response to "How Can You Tell if a Graph Is a Function"
Post a Comment